Funkcje Liniowe
Funkcją nazywamy takie przyporządkowanie, w którym
każdemu elementowi ze zbioru x jest przyporządkowany dokładnie Jeden
element ze zbioru y.
1.Wzór ogólny funkcji liniowej. y=a*x+b
a -Współczynnik
kierunkowy
b-wyraz
wolny
x - zmienna niezależna, argument funkcji
y - zmienna zależna, wartość funkcji
Wykresem funkcji
liniowej jest linia prosta.
Jest to funkcja
różnowartościowa czyli nie ma takich
dwóch argumentów x dla których funkcja
by przyjmowała tą samą wartość y.
2.a Monotoniczność funkcji w
zależności od
"współczynnika kierunkowego" a
funkcja rosnąca a>0
funkcja malejąca a<0
funkcja stała a=0
2.b Miejsca zerowe
-b:a
2.c Punkty przecięcia z osiami:
Punkt przecięcia z osią ox (-b:a;0)
Punkt przecięcia z osią oy (0;b)
2.d
Funkcja przyjmuje wartości "y":
gdy:
a>0
ujemne dla argumentów "x" (; -b:a)
-b:a)
dodatnie dla argumentów "x"(-b:a; )
)
gdy a<0
dodatnie dla argumentów "x" ( -b:a)
-b:a)
ujemne dla argumentów "x"(-b:a; )
)
2.e Kąt nachylenia funkcji liniowej do osi ox = 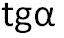 współczynnikowi kierunkowemu przy
a>0,
natomiast w a<0 kont nachylenia jest
ujemny.
współczynnikowi kierunkowemu przy
a>0,
natomiast w a<0 kont nachylenia jest
ujemny.
2.f Funkcje w których przynajmniej jeden
współczynnik jest równy = 0
a=0,b>0
wykresem funkcji jest linia prosta równoległe do osi ox,
przechodząca
nad osią ox przez I i II ćwiartke układu
współrzędnych.
a=0,b<
0, wykresem
funkcji jest prosta przechodząca pod osią ox,
równolegle do osi ox przez III i IV
ćwiartke
układu współrzędnych.
a>0,b=0,
wykresem
funkcji jest linia prosta przechodząca przez początek układu
współrzędnych i przez I i III ćwiartke układu
współrzędnych.
a<0,b=0,
wykresem
funkcji test linia prosta, przechodząca przez początek układu
współrzędnych i przez II i IV ćwiartke układu
współrzędnych.
2.f. Ćwiartki układu
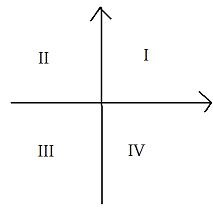
Ćwiartki układu współrzędnych oznaczamy
w kierunku
przeciwnym do ruchu wskazówek zegara, zaczynając od
"północnego zachodu", czyli od ćwiartki, w której
obie współrzędne są dodatnie.
2.g Prostopadłość, równoległość:
Dwie funkcje są prostopadłe wtedy i tylko wtedy gdy iloczyn
ich współczynników kierunkowych a1*a2
jest równy -1.
Dwie funkcje są względem siebie
równoległe wtedy i tylko wtedy gdy a1=a2.
y=a1*x+b1
y=a2*x+b1
Przekształcenie wykresu.
Wzóry=a(x-p)+b+q
gdzie;
p- przesunięcie poziome
p>0 w prawo
p<0 w
lewo
q - przesunięcie pionowe
q>0 w górę
q<0
w
dół
ZADANIA
Zadanie1
Narysuj wykres funkcji liniowej dla f(x)
y=2x+1, sporządź tabelkę, określ monotoniczność, oblicz miejsca zerowe
punkty przecięcia z osiami oraz przedziały, w których
funkcja przyjmuje wartości dodatnie i ujemne.
Zadanie2
Zadanie3
Zadanie4
Zadanie5
Zadanie6
Darmowy hosting zapewnia PRV.PL
 -
- -
- )
) -
- )
)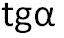 współczynnikowi kierunkowemu przy
współczynnikowi kierunkowemu przy
