Zadanie 6
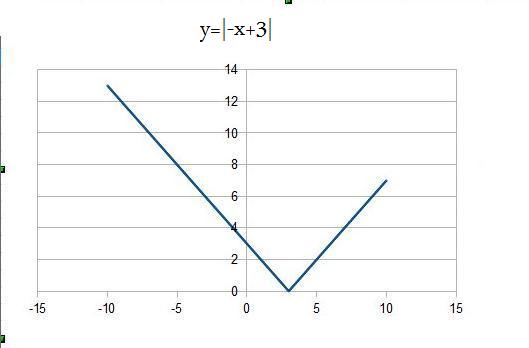
Naszkicuj wykres funkcji y=|-x+3| w przedziale (-10;10) i
następnie sprawdź dla jakich argumentów funkcja przyjmuje
wartośc 5, 12, 20, 28, 11
Wyłanczamy minus przed wartośc bewzględną.
-|x-3|
Następnie zamieniamy symbol wartości bezwzględnej nawiasem:
-(x-3)y=-x+3
Taki wzór funkcji będzie do argumentu +3 czyli do
miejsca zerowego, następnie wzór ten zamieniamy na:
y=x+3
Czyli funkcja z malejącej przechodzi w rosnącą
| x |
-10 |
-9 |
-8 |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| y |
13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Obliczamy argument funkcji dla wyżej wymienionych wartości i
do wartości do nich przeciwnych, które przyjęła by funkcja
gdyby nie było wartości bezwzględnej.
5
5
|-x+3|=5
-x+3=5
-x=5-3
-x=2/(-1)
x=-2-5
|-x+3|=-5
-x+3=-5
-x=-5-3
-x=-8\-1
x=8
12
12
|-x+3|=12
-x+3=12
-x=12-3
-x=9\(-1)
x=-9
|-x+3|=-12
-x+3=-12
-x=-12-3
-x=-15\(-1)
x=15
20
20
|-x+3|=20
-x+3=20
-x=20-3
-x=17\(-1)
x=-17
|-x+3|=-20
-x+3=-20
-x=-20-3
-x=-23\(-1)
x=23
28
28
|-x+3|=28
-x+3=28
-x=28-3
-x=25\(-1)
x=-25
|-x+3|=-28
-x+3=-28
-x=-28-3
-x=-31\(-1)
x=31
11
11
|-x+3|=11
-x+3=11
-x=11-3
-x=8\(-1)
x=-8
|-x+3|=-11
-x=-11-3
-x=-14\(-1)
x=14
Jak można łatwo zauważyc te argumenty są symetryczne względem
x=3 czyli względem osi symetrii biegnącej przez punkt (3;0) czyli przez
miejsce zerowe funkcji.
Darmowy hosting zapewnia PRV.PL
