Zadanie 5
Wyznacz wzór funkcji równoległej do
funkcji
y=2x+4, przechodzącej przez punkt (-2;-8), naszkicuj wykres w przedziale
(-5;5), zbadaj jej monotoniczność, przedziały w których
przyjmuje wartości dodatnie i ujemne, znajdź miejsce zerowe, miejsca
przecięcia z osiami x i y, określ jaki to rodzaj funkcji, tj. rosnąca
maleją czy stała.
Przywołujemy wzór na równoległość
a1=a2
y=2x+b
Podstawiamy do wzoru x=(-2) y=(-8); a2=2;
(-8)=2*x+b
(-8)=2*(-2)+b
(-8)=(-4)+b
Uporządkowujemy wyrazy
(-b)=(-4)+8
(-b)=4
Mnożymy przez (-1) w celu pozbycia się ujemności.
-b=4*(-1)
b=(-4)
Powstaje nam wzór.
y=2x-4
x
| x |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
| y |
-14 |
-12 |
-10 |
-8 |
-6 |
-4 |
-2 |
0 |
2 |
4 |
6 |
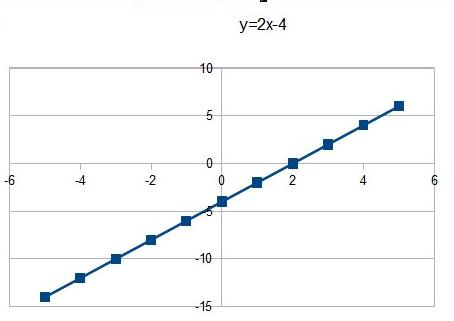
><0 - funkcja rosnąca
Miejsce zerowe: (-b\a;0)
2x-4=0
2x=4\2
x=2
Funkcja przyjmuje wartości ujemne dla argumentów ( ;2).
;2).
Funkcja przyjmuje
wartości dodatnie dla argumentów (2; ).
).
Miejsca przecięcia z osiami
z osią x
(-b\a;0)
(-(-4\2);0)
(2;0)
Miejsce przecięcia z osią y(0;b)
(0,(-4))
Darmowy hosting zapewnia PRV.PL
 ;2).
;2).
 ;2).
;2). ).
).