Zadanie 1
Narysuj wykres funkcji liniowej dla f(x) y=2x+1, sporządź
tabelkę, określ monotonicznośc, oblicz miejsca zerowe, punkty przecięcia
z osiami oraz przedziały, w których funkcja przyjmuje
wartości dodatnie i ujemne.
Obliczamy wartość y dla argumentów f(x)
(-10;9) np f(-10)=2*(-10)+1=(-19)
f(-9)=2*(-9)+1=(-17)f(-8)=2*(-8)+1=(-15) itd, aż do argumentu 9
f(9)następnie na podstawie tych obliczeń rysujemy wykres funkcji f(x),
później graf,
f(x)=2*x+1
| x |
y |
| -10 |
-19 |
| -9 |
-17 |
| -8 |
-15 |
| -7 |
-13 |
| -6 |
-11 |
| -5 |
-9 |
| -4 |
-7 |
| -3 |
-5 |
| -2 |
-3 |
| -1 |
-1 |
| 0 |
1 |
| 1 |
3 |
| 2 |
5 |
| 3 |
7 |
| 4 |
9 |
| 5 |
11 |
| 6 |
13 |
| 7 |
15 |
| 8 |
17 |
| 9 |
19 |
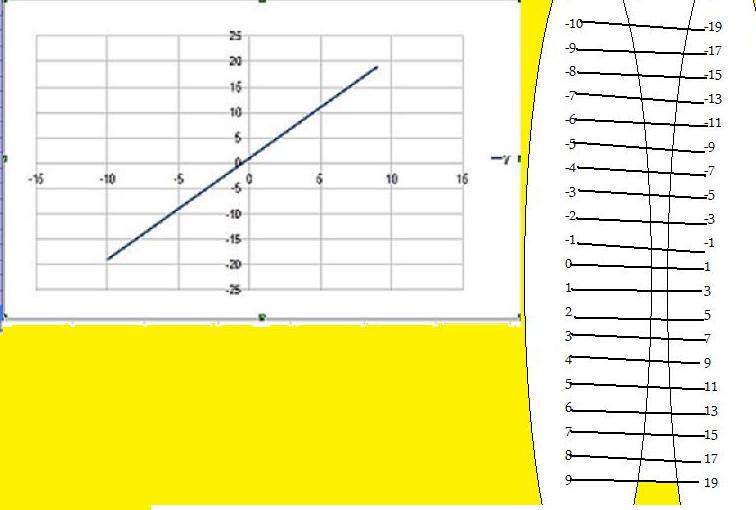
Na podstawie tej funkcji możemy ocenic, że jest ona
rosnąca, ponieważ a>0 i wraz ze wzrostem argumentów
funkcja "unosi" się w górę, rośnie jej wartośc. punkt
przecięcia z osią ox (-b:a;0) = (-1:2;0)=(-1\2;0)- miejsce zerowe,
punkt przecięcia z osią oy (0;b) = (0;1).
Funkcja przyjmuje wartości ujemne dla argumentów (
;-1\2).
Funkcja przyjmuje wartości dodatnie dla argumentów (-1\2;
)
Darmowy hosting zapewnia PRV.PL