

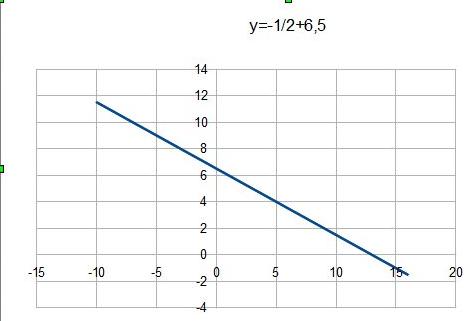
| x | -10 | -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| y | 11,5 | 11 | 10,5 | 10 | 9,5 | 9 | 8,5 | 8 | 7,5 | 7 | 6,5 | 6 | 5,5 | 5 | 4,5 | 4 | 3,5 | 3 | 2,5 | 2 | 1,5 | 1 | 0,5 | 0 | -0,5 | -1 |
 ;13).
;13). ).
).
W trosce o komfort korzystania z naszego serwisu chcemy dostarczaÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ Ci coraz lepsze usÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂugi. By mÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂc to robiÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ prosimy, abyÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂø wyraziÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ zgodÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ na dopasowanie treÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂøci marketingowych do Twoich zachowaÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ w serwisie. Zgoda ta pozwoli nam czÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂøciowo finansowaÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ rozwÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂj ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂøwiadczonych usÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂug.
PamiÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂtaj, ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂe dbamy o TwojÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ prywatnoÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂøÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂ. Nie zwiÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂkszamy zakresu naszych uprawnieÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ bez Twojej zgody. Zadbamy rÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂwnieÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂ o bezpieczeÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪stwo Twoich danych. WyraÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂonÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ zgodÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ moÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂesz cofnÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÝ̪ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ w kaÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂÄÂÄšÄÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂÄÂĂÂÄÂĂÂĂÂĂÂÄÂĂ ĂÂĂÂÄÂĂÂĂÂĂÂÄÂĂÂĂÂĂÂĂĹĄĂÂĂÂĂÂÄÂĂÂdej chwili.