Funkcje kwadratowe
Funkcją nazywamy takie przyporządkowanie,
w którym każdemu elementowi ze zbioru x jest
przyporządkowany dokładnie Jeden element ze zbioru y.
Wzór ogólny funkcji
kwadratowej
y=a2x+bx+c
Właściwości funkcji kwadratowych
Wykresem funkcji
kwadratowej jest parabola, składająca się z ramion
i wierzchołka funkcji.
a-Współczynnik
decydujący o
kierunku funkcji i monotoniczności.
b-
c- wyraz wolny, miejsce
przecięcia
funkcji z osiami oy.
x- zmienna niezależna, argument funkcji
y- zmienna zależna,
wartośc funkcji.
2.a Miejsce zerowe funkcji w zależności od ∆.
∆=b2-4*a*c
i wtedy w zależności od ∆.
Jeżeli:
∆<0 równanie
sprzeczne,
kończymy.
∆=0 równanie posiada jedno
rozwiązanie:
x=(-√∆)\2a
∆>0 - równanie posiada dwa
rozwiązania
x1=(-b-√∆)\2*a;
x2=(-b+√∆)\2*a
Współrzędne
wierzchołka (p;q)
gdzie:
p= (-b)\2a
lub (x1+x2)\2a
odpowiada za ox poziom x ,
q=-∆\4a
odpowiada za oy pion y
2b Monotoniczność funkcji w zależności od
wspołczynnika a
a>0
- Funkcja
jest malejąca w
przedziale ( ;p), funkcja jest
rosnąca w przedziale (p;
;p), funkcja jest
rosnąca w przedziale (p; ), funkcja
przyjmuje wartości dodatnie dla argumentów z
przedziału (
), funkcja
przyjmuje wartości dodatnie dla argumentów z
przedziału ( ;x1)∪(x2
;x1)∪(x2 ),
funkcja
przyjmuje wartości
ujemne dla argumentów z przedziału (x1;x2),
funkcja
przyjmuje wartośc minimum q dla argumentu równego
p.zbiór wartości (q;
),
funkcja
przyjmuje wartości
ujemne dla argumentów z przedziału (x1;x2),
funkcja
przyjmuje wartośc minimum q dla argumentu równego
p.zbiór wartości (q; ).
).
a<0
- Funkcja
jest rosnąca w przedziale ( ;p),
funkcja
jest malejąca w przedziale (p;
;p),
funkcja
jest malejąca w przedziale (p; ), funkcja przyjmuje wartości
ujemne dla argumentów z
przedziału (
), funkcja przyjmuje wartości
ujemne dla argumentów z
przedziału ( ;x2)∪(x2
;x2)∪(x2 ),
funkcja
przyjmuje wartości
dodatnie w przedziale (x1;x2),
funkcja
przyjmuje wartośc q maksimum dla argumentu p. zbiór
wartości (
),
funkcja
przyjmuje wartości
dodatnie w przedziale (x1;x2),
funkcja
przyjmuje wartośc q maksimum dla argumentu p. zbiór
wartości ( ;q).
;q).
a>0
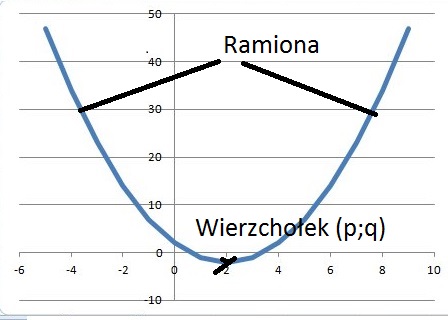 a<0
a<0
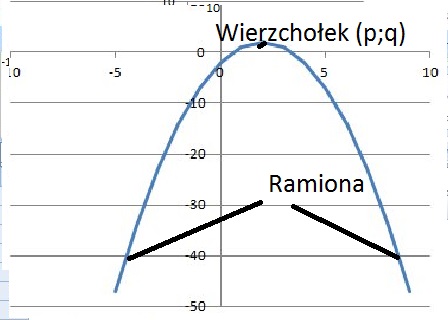
2.c Punkty przecięcia z osiami
Przecięcie z osią ox(miejsca zerowe
funkcji) punkty: (x1;0), (x2;0)
Przecięcie
z osiami oy punkt (o;c)
2.d Funkcje w których przynajmniej jeden ze
współczynników b lub c =0
Gdy b = 0 wierzchołek
funkcji znajduje
się na osi oy, jest to tak zwana funkcja parzysta f(x)=f(-x)
czyli taka, w której przeciwne argumenty mają tą
samą wartość.
Gdy c = 0 jednym z miejsc zerowych funkcji jest
punkt (0;0)
2.e Postacie funkcji kwadratowych.
Postać ogólna funkcji kwadratowej ax2+bx+c
Postać
iloczynowa funkcji kwadratowej a(x-x1)(x-x2)dla
∆=0 a(x-x1)2
Postać
kanoniczna funkcji kwadratowej a(x-p)2+q
Wzory Viete'a
suma rozwiązań x1+x2=(-b/a)
Iloczyn rozwiązań x1*x2=(c/a)
Zadania
Zadanie1
Zadanie2
Zadanie3
Zadanie4
Zadanie5
Zadanie6
Darmowy hosting zapewnia PRV.PL
 ;p), funkcja jest
rosnąca w przedziale (p;
;p), funkcja jest
rosnąca w przedziale (p; ), funkcja
przyjmuje wartości dodatnie dla argumentów z
przedziału (
), funkcja
przyjmuje wartości dodatnie dla argumentów z
przedziału ( ;x1)∪(x2
;x1)∪(x2 ),
funkcja
przyjmuje wartości
ujemne dla argumentów z przedziału (x1;x2),
funkcja
przyjmuje wartośc minimum q dla argumentu równego
p.zbiór wartości (q;
),
funkcja
przyjmuje wartości
ujemne dla argumentów z przedziału (x1;x2),
funkcja
przyjmuje wartośc minimum q dla argumentu równego
p.zbiór wartości (q; ).
).
