Strona Główna Funkcje kwadratowe Moja matma Moja choroba

Zadanie1

Mając funcje: x²-10x+4=0, określ przedziały monotoniczności, zbiór wartości i zapisz funkcje w trzech postaciach to jest ogólnej, iloczynowej i kanonicznej.

wzór postaci ogólnej funkcji:

ax²bx+c=0

Piszemy wzór funkcji

x²-10x+4=0

Współczynniki: a=1; b=10; c=4

b²-4*a*c=0

100-4*1*4=0

100-16=0

84=0

∆=84

√∆=√(84)

√∆=√(4*21)

√∆=2√(21)

Obliczamy pierwiastek x₁

x₁=(-b-√∆)\(2*a)

x₁=(-(-10)-2√(21))\(2*1)

x₁=(10-2√(21))\2

wyłączamy  2 przed nawias

x₁2(5-√(21))\(2*1)

Skracamy

x₁=2(5-√(21))\2

x₁₌5-√(21)

Obliczamy x₂

x₂=(-b-√∆)\(2*a)

x₂=(-(-10)+2√(21))\(2*1)

x₂(10+2√(21)\2

wyłączamy  2 przed nawias

x₂=2(5+√(21))\2

Skracamy

x₂=2(5+√(21))\2

5+√(21)

Miejsca zerowe funkcji

x₁=5-√(21)

x₂=5+√(21)

Zapisujemy wzór w postaci iloczynowej

a(x-x₁)(x-x₂)

(x-(5+√(21))(x-(5-√(21))

(x-5-√(21))(x-5+√(21))

Obliczamy współrzędne p i q

p=-b\(2*a)
p=-(-10)\(2*1)

p=10\2

p=5

Obliczamy współrzędne wierzchołka q

q=-∆\(4*a)

q=(-84)\(4*1)

q=(-21)

Współrzędne wierzchołka (p;q); (5;(-21))

Postać kanoniczna funkcji

(x-p)²+q

(x-5)²-21

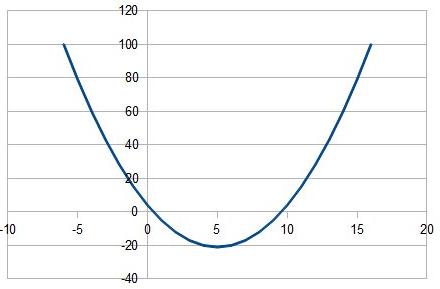
a>0 funkcja przyjmuje minimum o wartości (5;(-21))

Funkcja przyjmuje wartości dodatnie w przedziale (;5-√(21));∪(5+√(21);)

Funkcja przyjmuje wartości ujemne w przedziale (5-√(21);5+√(21))

Funkcja jest malejąca w przedziale (;5)

Funkcja jest rosnąca w przedziale (5;)

Zbiór wartości (-21;)

Do góry Strona Główna Funkcje kwadratowe Moja matma Moja choroba