Zadanie 6
Oblicz:
a)Dlugość boków prostokąta wiedząc, że jeden z
jego boków jet o 4 cm dłuższy od drugie i ma on pole 96 cm2
b)Długość boków działki o powierzchni 6
arów wiedząc, że jeden z jego boków jest o 10m
dłuższy od drugiego
a)Rysunek pomocznicy

Dane:
a=x cm; b=x+4 cm; P=96 cm2
Szukane
x?
Korzystamy ze wzoru na pole prostokąta
P=a*b
Podstawiamy
96=x(x+4)
96=x2+4x
Przenosimy wszystko na lewą stronę a po prawej piszemy 0 oraz
uporządkowujemy w kolejności malejącej potęgi, powstaje nam
równanie kwadratowe.
-x2-4x-96=0
Parametry: a= (-1); b=(-4); c=96
∆=b2-4*a*c=
∆=(-4)2-4*(-1)*96=
∆=16-(-384)=
∆=16+384=
∆=400
√∆=20
Obliczamy x1 i x2
i sprawdzamy, które z nich jest rozwiązanie
równania (warunek x>o)
x1=(-b-√∆)/2*a
x1=(-(-4)-√400)/2*(-1)
x1=(4-20)/2*(-1)
x1=(-16)/(-2)=8
x1=4; x1>0
by się zgadzało, ale sprawdzimy jeszcze x2
x2=(-b+√∆)/2*a
x2=(-(-4)+√400)/2*(-1)
x2=(4+20)/(-2)
x2=24/(-2)
x2=(-12)
x2<0 - równanie
sprzeczne, czyli x1 jest rozwiązaniem
równania. prostokąt ma następującej długości boki:
x = 4x+4=12
P=96
L =8*12
L=96
L=P
b)Rysunek pomocniczy
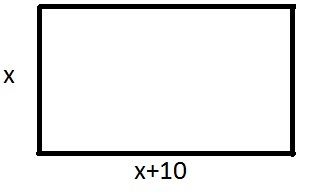
Dane:
a= x m; b= x+10 m; P= 6 arów = 600m2
Szukane
x?
Korzystamy ze wzoru na pole prostokąta
P=a*b
Podstawiamy:
600=x(x+10)
600=x2+10x
Przenosimy wszystko na lewą stronę, a po prawej piszemy 0
oraz uporządkowujemy w kolejności malejącej potęgi, powstaje nam
równanie kwadratowe.
-x2-10x-600=0
Parametry: a=(-1) b=(-10) c=600
∆=b2-4*a*c
∆=102-4*(-1)*600
∆=100+2400
∆=2500
√∆=50
Obliczamy x1 i x2
i sprawdzamy, które z nich jest rozwiązaniem
równania (warunek x>0)
x1=(-b-√∆)/2*a
x1=(-(-10)-√2500)/2*(-1)
x1=(10-50)/2*(-1)
x1=(-40)/(-2)
x1=20
x1>0 by się zgadzało, ale
sprawdzimy jeszcze x2.
x2=(-b+√∆)/2*a
x2=(-(-10)+√2500)/2*(-1)
x2=(10+50)/(-2)
x2=60/(-2)
x2=(-30)
x2 nie jest rozwiązaniem
równania poniewż x2<0
Działka ma następujące długości:
x=20x+10=
20+10=30
P=600
L=20*30
L=600
L=P
Darmowy hosting zapewnia PRV.PL

