Strona Główna Funkcje kwadratowe Moja matma Moja choroba

Zadanie 2

Dla jakich argumentów funkcja f(x)=-2x²-8x+6 przyjmuje wartośc (-18), oraz f(x)>(-18) i f(x)<(-18).

Wzór ogólny funkcji

ax²+bx+c

Podstawiamy do wzoru.

-2x²-8x+6=0

Obliczamy dla jakich argumentów funkcja przyjmuje wartość (-18).

-2x²-8x+6=(-18)

Przenosimy wartośc (-18) z lewej strony na prawą.

-2x²-8x+6-18=0

-2x²-8x+24=0

Wyłączamy 2 przed nawias.

2(-x²-4x+12)=0

-x²-4x+12=0

Obliczamy ∆:

 Parametry: a=(-1); b=(-4); c= 12;

∆=b²-4*a*c

∆=(-4)²-4*(-1)*12

∆=16-(-48)

∆=16+48

∆=64

√(∆)=√64

∆=8

Obliczam x₁ czyli pierwszy argument funkcji, dla którego funkcja przecina się z prostą y =(-18).

x₁=(-b-√(∆))\(2*a)

x₁=(-(-4)-8)\(2*(-1))

x₁=(4-8)\(-2)

x₁=(-4)\(-2)

x₁=2

Obliczamy x₂ czyli drugi argument dla, którego funkcja przecina się z prostą y=(-18)

x₂=(-b+√(∆))\(2*a)

x₂=(-(-4+8)\(2*(-1))

x₂=(4+8)\(-2)

x₂=12\(-2)

x₂=(-6)

Funkcja f(x) przecina się z prostą y=(-18) w punktach [-6;(-18)] i [(2);(-18].Czyli argument (-6) i dwa są argumentami dla których funkcja przyjmuje wartość (-18).

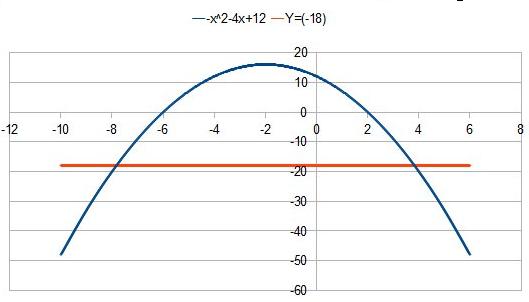
Uwaga powyższe punkty obliczone są dla przecięcia się funkcji kwadratowej z prostą y=(-18), nie należy mylić tego z miejscami zerowymi. Funkcja przyjmuje wartości mniejsze od prostej y = (-18) dla argumentów (;(-6))∪(2;)Funkcja kwadratowa przyjmuje wartości większe od prostej y= (-18) dla argumentów ((-6);2).

Do góry Strona Główna Funkcje kwadratowe Moja matma Moja choroba