Strona Główna Funkcje kwadratowe Moja matma Moja choroba

Zadanie3

Wyznacz wzór funkcji kwadratowej wiedząc, że ma ona wierzchołek o współrzędnych (3;1) i przechodzi przez punkt (5;-3), zapisz tą funkcję we wszystkich trzech postaciach: to jest ogólnej kanonicznej i iloczynowej, określ przedziały monotoniczności funkcji, zbiór wartości oraz argumenty, dla których funkcja przyjmuje wartości dodatnie i ujemne.

Wykorzystujemy postać kanoniczną funkcji w celu obliczenia współczynnika a: p=3; q=1; x=5; y=-3;

y=a(x-p)²+q 

y=a(x-3)²+1

-3=a(5-3)²+1

-3=a2²+1

-3=4a+1

Uporządkowujemy

-4a=1+3

-4a=4

Dzielimy przez (-4) w celu pozbycia się ujemności żebyśmy mieli a = 1

-4a=4\(-1)

a=(-1)

Wykorzystujemy postac kanoniczną w celu wyprowadzenia postaci ogólnej, piszemy (-) przed nawiasem ponieważ a=(-1), korzystamy ze wzoru skróconego mnożenia (x-p)²=x²-2*x*p+²=x²-2xp+p²

y=-(x-3)²+1

-(x²-2*x*3+3²)+1

-(x²-6x+9)+1

-x²+6x-9+1

-x²+6x-8

Wyprowadzamy postać iloczynową korzystając z postaci ogólnej

-x²+6x-8

Współczynniki a=(-1); b=6; c=(-8)
Obliczam ∆

∆=b²-4*a*c

∆=6²-4*(-1)*(-8)

∆=36-32

∆=4

√(∆)=4

√(4)=2

Obliczam pierwszy pierwiastek x₁

x₁=(-b-√(∆))\(2*a)

x₁=(-6-2)\(2*(-1))

x₁(-8)\(-2)

x₁=4

Obliczam pierwiastek x₂

x₂=(-b+√(∆))\(2*a)

x₂=(-6+2)\(2*(-1))

x₂=(-4)\(-2)

x₂=2

Zapisuje wzór w postaci iloczynowej pamiętając o minusie przed nawiasem gdyż a=(-1)

a(x-x₁)(x-x₂)

-(x-4)(x-2)

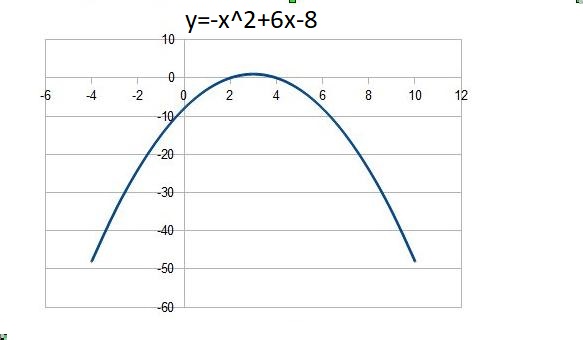
Przedziały monotoniczności funkcji

Funkcja jest rosnąca w przedziale (;3)

Funkcja jest malejąca w przedziale (3;)

Funkcja przyjmuje wartości ujemne dla argumentów z przedziału (;2)∪(4;)

Funkcja przyjmuje wartości dodatnie dla argumentów z przedziału (2;4)

Zbiór wartości (;1)

Do góry Strona Główna Funkcje kwadratowe Moja matma Moja choroba