WielomianyWzór ogólny
wielomianówanxn+an-1xn-1+an-2xn-2.....a2x2+a1x1+a0
Wielomianyanxn........+a0
gdzie:
an-
Współczynnik przy najwyższej
potędze, decyduje o kierunku funkcji wielomianowej, (jego znak decyduje
o
wartości jaką przyjmuje funkcja wielomianowa od pierwiastka najbardziej
położonego na prawo do  )
)
n- Stopień wielomianu.
a0-
wyraz wolny decyduje o miejscu przecięcia się funkcji wielomianowej z
osią oy.
Jednomian
axn
gdzie:
a- Współczynnik
jednomianu
n - Stopień jednomianu
Właściwości wielomianów
Wielomiany składają się z jednomianów,
czyli
poszczególnych współczynników wraz ze
stopniami.
Jednomiany oraz w całości wielomiany można monożyć i dzielić, natomiast
dodawać i odejmować można tylko wielomiany, które mają w
sobie
jednomiany o tych samych stopniach i tylko ich współczynniki
(parametry) można dodawać i odejmować.
Mnożenie wielomianów
ai*bj=abi+j
Dzielenie wielomianów
ai:bj=a\bi-j
Postać iloczynowa wielomianów
a(x-x1)(x-x2(x-x3).......(x-xn)
a- decyduje o monotoniczności
wielomianu
x1,x2,x3,xn
- pierwiastek wielomianu
Pierwiastki wielomianu
Liczba p jest pierwiastkiem wielomianu W(x) wtedy i
tylko wtedy, gdy wielomian W(x) jest podzielny przez dwumian (x-p)
Krotności
(x-p)k
gdzie
k - Krotność czyli ilość z jaką dany
pierwiastek występuje w wielomianie
p - pierwiastek wielomianu
Rozkład wielomianu
Za rozkład wielomianu na czynniki (pierwiastki)
odpowiada schemat Hornera
|
an |
an-1 |
an-2 |
an-3 |
an-4 |
.. |
.. |
.. |
a3 |
a2 |
a1 |
a0 |
| p1 |
an |
ak3w2=p1*an+an-1 |
ak4w2=p1*ak3w2+an-2 |
ak5w2=p1*ak4w2+an-3 |
ak6w2=p1*ak5w2+an-4 |
.. |
.. |
.. |
ak7w2=p1*ak6w2+a3 |
ak8w2=p1*ak7w2+a2 |
ak9w2=p1*ak8w2+a1 |
ak10w2=p1*ak9w2+a0=0 |
| p2 |
an |
ak3w3=p2*an+ak3w2 |
ak4w3=p2*ak3w3+ak4w2 |
ak5w3=p2*ak4w3+ak5w2 |
ak6w3=p2*ak5w3+ak6w2 |
.. |
.. |
.. |
ak7w3=p2*ak6w3+ak7w2 |
ak8w3=p2*ak7w3+ak8w2 |
ak9w3=p2*ak8w3+ak9w2=0 |
| p3 |
an |
ak3w4=p3*an+ak3w3 |
ak4w4=p3*k3w4+ak4w3 |
ak5w4=p3*ak4w4+ak5w3 |
ak6w4=p3*ak5w4+ak6w3 |
.. |
.. |
.. |
ak7w4=p3*ak6w4+ak7w3 |
ak8w4=p3*ak7w4+ak8w3=0 |
| p4 |
an |
ak3w5=p4*an+ak3w4 |
ak4w5=p4*ak3w5+ak4w4 |
ak5w5=p4*ak4w5+ak5w4 |
ak6w5=p4*ak5w5+ak6w4 |
.. |
.. |
.. |
ak7w5=p4*ak6w5+ak7w4=0 |
| ... |
... |
................ |
................ |
................ |
................ |
.. |
.. |
.. |
| ... |
... |
................ |
................ |
................ |
................ |
.. |
.. |
| ... |
... |
................ |
................ |
................ |
................ |
.. |
| p5 |
an |
ak3w6=p5*an+ak3w5 |
ak4w6=p5*ak3w6+ak4w5 |
ak5w6=p5*ak4w6+ak5w5 |
ak6w6=p5*ak5w6+ak6w5=0 |
| p6 |
an |
ak3w7=p6*an+ak3w6 |
ak4w7*p6*ak3w7+ak4w6 |
ak5w7=p6*ak4w7+ak5w6=0 |
| p7 |
an |
ak3w8=p7*an+ak3w7 |
ak4w8=p7*ak3w8+ak4w7=0 |
W pierewszym wierszu znajdują się
współczynniki,
natomiast w pierwszej kolumnie znajdują się potencjalne pierwiastki
dzielniki wyrazu wolnego (w przypadku pierwiastków
całkowitych)
lub iloraz wyrazu wolnego i współczynnika przy najwyższej
potędze w (przypadku pierwiastków wymiernych) W indeksie
dolnym
zapisano położenie danej komórki
względem pustej komórki na górze w (lewym rogu),
symbol k
oznacza numer kolumny, natomiast symbol w numer wiersza. Wyraz an
jest ciągle ten sam, natomiast wyraz wolny ao
znajduje się w przedostatniej rozwiązanej komórce danego
wiersza
(ponieważ ostatni zawsze musi równac się 0).
Uogólniając
mnożymy potencjalny pierwiastek przez wartość poprzedniej
komórki i dodajemy do tego wartość współczynnika
znajdującego się w tej samej kolumnie. W każdym wierszu jest o
dokładnie jeden współczynnik
mniej niż w poprzednim. Operację tą prowadzimy do momentu gdy będziemy
mieli 3 wyrazy (równanie kwadratowe), lub szybciej, gdy
wzory
skróconego mnożenia pozwolą go rozłożyc na czynniki.
Oczywiście
kolumna ta może mieć inne rozmiary, większe lub mniejsze, w tym właśnie
celu zostawiliśmy kropki w tabeli.
Wykresy funkcji wielomianowych
an
współczynnik przy najwyższej potędze
decyduje o tym jakie wartości będzie przyjmowała funkcja od pierwiastka
znajdującego się najbardziej na prawo (od współrzędnej
(0;0)) do Dla an>0
Dla an>0
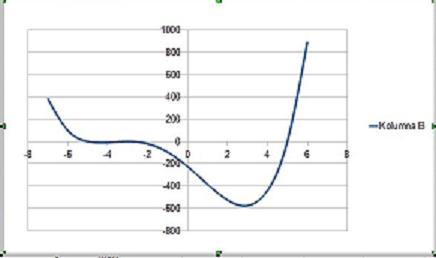
Dla an<0
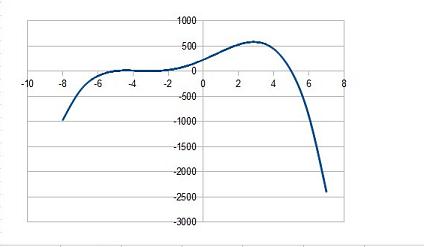
Początek wykresu (patrząc od prawej) Dla an>0
Dla an<0
Wykres funkcji
Wykres funkcji zawsze rysujemy od prawej
strony
Krotność pierwiastka
Wspomniana wcześniej krotność (k) pierwiastka ma
wpływ na
przebieg wykresu Wyróżniamy pierwiastki parzystokrotne i
nieporzystokrotne.
Parzystokrotne - wykres funkcji nie przechodzi na
przeciwną
stronę osi liczbowej, ani przez oś ox w układzie
współrzędnych
(wiem, że wykresy są tylko uproszczone).
Funkcja nadal przyjmuje wartości dodatnie.

Funkcja nadal przyjmuje wartości ujemne.

Nieparzystokrotne - wykres funkcji przechodzi na
przeciwną stronę osi liczbowej lub przez oś ox w układzie
współrzędnych.
Funkcja zmienia przyjmowane przez siebie wartości z
dodatnich na ujemne (patrząc od prawej strony).

Funkcja zmienia przyjmowane przez siebie wartości z
ujemnych na dodatnie (patrząc od prawej strony).

Pochodna funkcji wielomianowej
Dotychczasowe informacje pozwalają nam określić w
jakich
przedziałach funkcja przyjmuje wartość dodatnią lub ujemną, natomiast
nie pozwalają nam określić w jakich przedziałach funkcja jest rosnąca,
malejąca lub stała, żeby to określić musimy mieć tzw. pochodną funkcji
wielomianowej.
funkcja f(x)= anxn+an-1xn-1+an-2xn-2.....a2x2+a1x1+a0
Pochodna funkcji f(x) Ekstema
f(x)'= n*anxn-1+(n-1)*an-1xn-2+(n-2)*an-2xn-3....2*a2x1+a1x
Wnioski
Pochodną (ekstrema) obliczamy w następujący
sposób: każdy ze stopni
jednomianu przemnażamy przez jego współczynnik, a następnie
stopień jednomianu w indeksie górnym pomniejszamy o jeden.
Wyrazem wolnym pochodnej jest dotychczasowy wyraz funkcji wyjściowej a1(czyli
parametr stojący przy x w funkcji wyjściowej), następnie obliczamy
pierwiastki tej pochodnej (korzystając np. ze schematu Horrnera) i
nanosimy je na oś liczbową.
Funkcja jest rosnąca w przedziale w,
którym jej pochodna przyjmuje wartości dodatnie.
Funkcja jest maleją przedziale, w którym
jej pochodna przyjmuje wartości ujemne.
Funkcja przyjmuje maksimum lokalne w punkcie w
którym wartość pochodnej przechodzi z dodatniej w ujemną.

Funkcja przyjmuje minimum lokalne w punkcie, w
którym wartość pochodnej przechodzi z ujemnej w dodatnią.

Jeśli mamy parzysty pierwiastek pochodnej
mówimy, że
jest to punkt przegięcia funkcja przechodzi z jednej strony stycznej na
drugą.


Gdy już mamy pierwiastki pochodnej możemy je
podstawić do
wyjściowego wzoru funkcji f(x) w celu abliczenia wartości lokalnych
minimum i maksimum oraz punktów przegięcia.
Zadania
Zadanie1
Zadanie 2
Zadanie3
Zadanie 4
Darmowy hosting zapewnia PRV.PL
 )
)  )
)  Dla an>0
Dla an>0