 ;-1)∪(-1/3;1)∪(2;
;-1)∪(-1/3;1)∪(2; )
)| 3 | -5 | -5 | 5 | 2 | |
| 1 | 3 | 1*3-5=3-5=(-2) | 1*(-2)-5=(-2)-5=(-7) | 1*(-7)+5=(-7)+5=(-2) | 1*(-2)+2=(-2)+2=0 |
| 3 | -2 | -7 | -2 | |
| (-1) | 3 | (-1)*3-2=(-3)-2=(-5) | (-1)*(-5)-7=5-7=(-2) | (-1)*(-2)-2=2-2=0 |
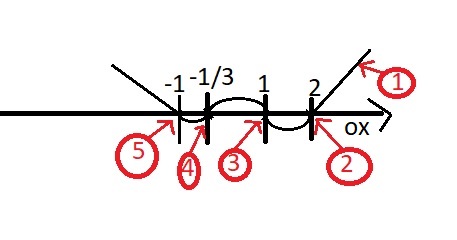
| Pierwiastek | Krotność | Parzystość/Nieparzystość | Przechodzi/Nie przechodzi |
| 2 | 1 | Nieparzystość | Przechodzi |
| 1 | 1 | Nieparzystość | Przechodzi |
| -1/3 | 1 | Nieparzystość | Przechodzi |
| -1 | 1 | Nieparzystość | Przechodzi |





 ;-1)∪(-1/3;1)∪(2;
;-1)∪(-1/3;1)∪(2; )
)| -1 | 8 | -21 | 18 | |
| 2 | -1 | 2*(-1)+8=(-2)+8=6 | 2*6-21=12-21=(-9) | 2*(-9)+18=(-18)+18=0 |
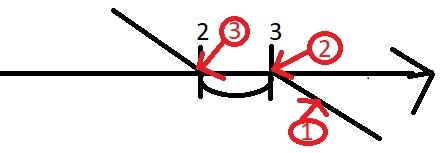
| Pierwiastek | Krotność | Parzystość/Nieparzystość | Przechodzi/Nie przechodzi |
| 3 | 2 | Parzystość | Nie przechodzi |
| 2 | 1 | Nieparzystość | Przechodzi |



 )
)