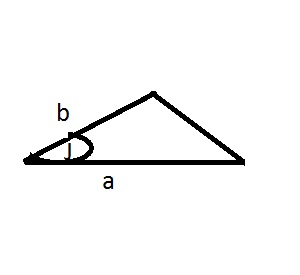
Funkcja
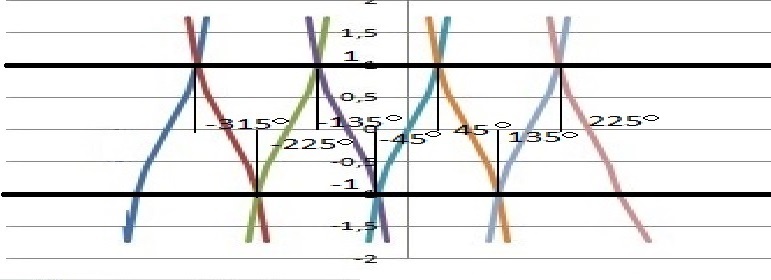
Funkcje
Funkcje
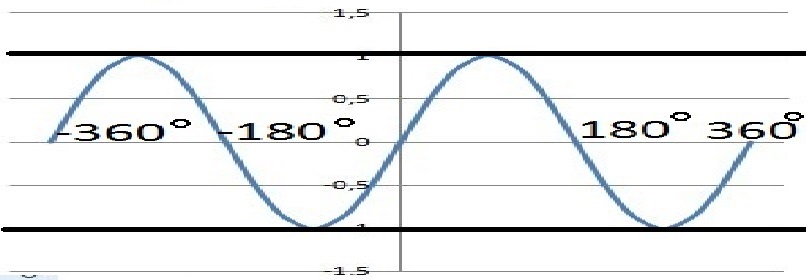
Funkcja
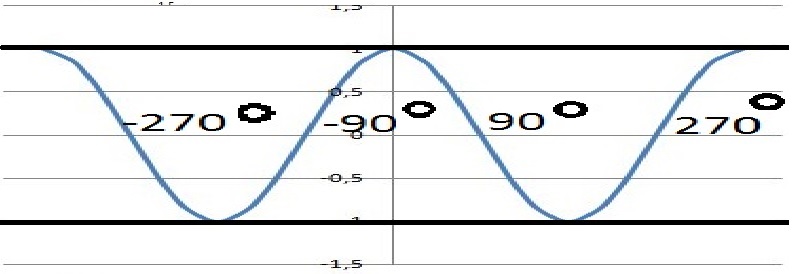
Funkcja
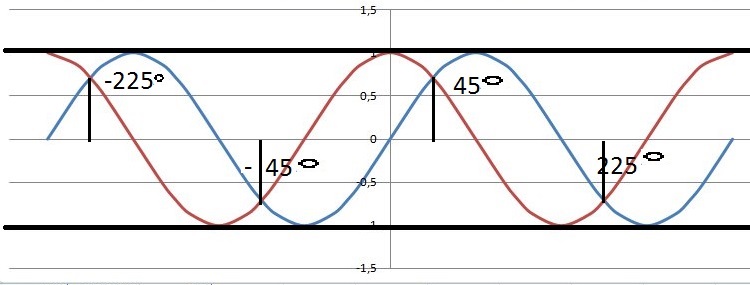
|
|
wartość bezwzględna
wartość bezwzględna
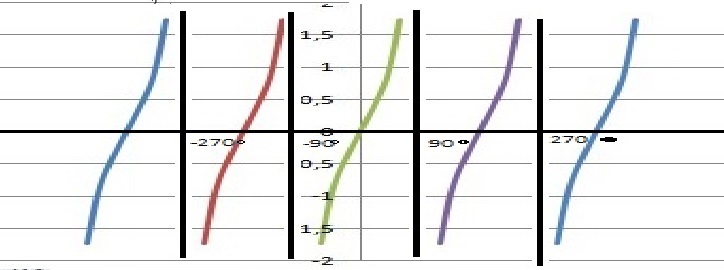
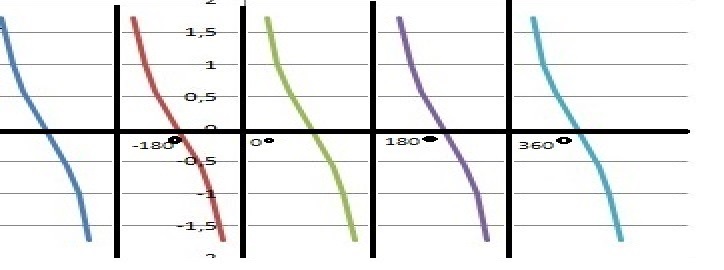
8.Wzory redukcyjne
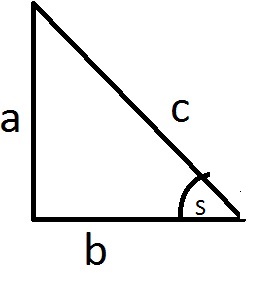
| w stopniach | 0⁰ | 30⁰ | 45⁰ | 60⁰ | 90⁰ | 180⁰ | 270⁰ | 360⁰ |
| w radianach | 0 | 1/6π | 1/4π | 1/3π | 1/2π | π | 3/2π | 2π |
| 0 | √(3)/3 | 1 | √(3) | nie istnieje |
0 | nie istnieje |
0 | |
| nie istnieje |
√(3) | 1 | √(3)/3 | 0 | nie istnieje |
0 | nie istnieje |
|
| 0 | 1/2 | √(2)/2 | √(3)/2 | 1 | 0 | -1 | 0 | |
| 1 | √(3)/2 | √(2)/2 | 1/2 | 0 | -1 | 0 | 1 |
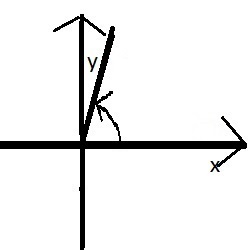
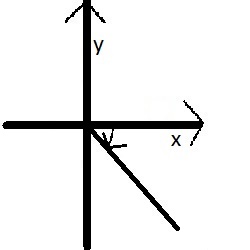
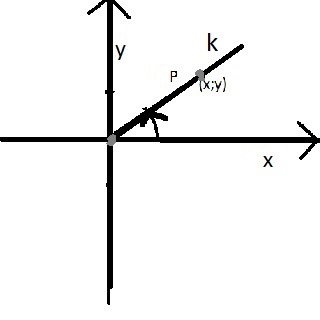
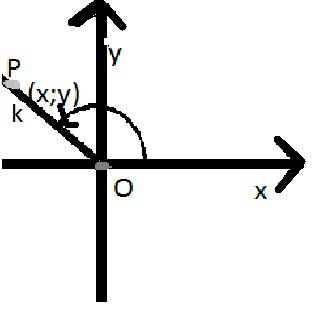
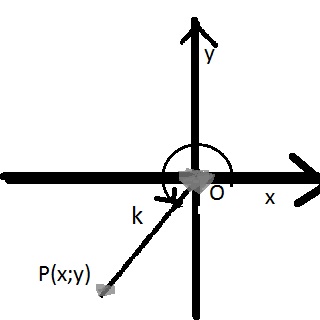
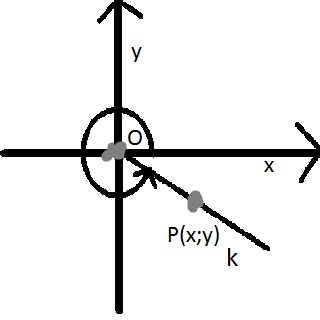
| w stopniach | 0o - 90o | 90o- 180o | 180o - 270o | 270o - 360o |
| w π | 0 - 1/2π | 1/1/2π - π | π - 3/2π | 3/2π - 2π |
| ćwiartki | I | II | III | IV |
| + | - | + | - | |
| + | - | + | - | |
| + | + | - | - | |
| + | - | - | + |